Исследование данных о приюте
Фильтрация и сортировка
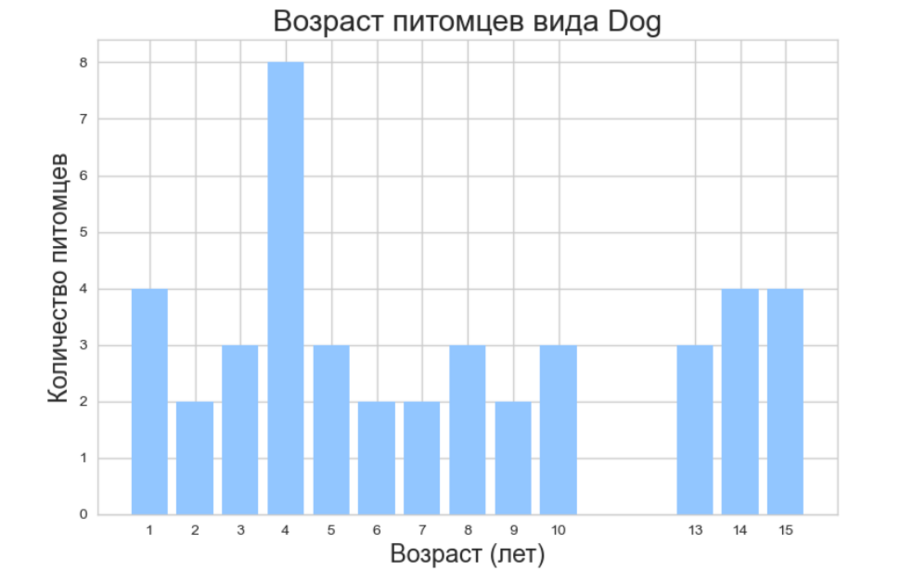
Фильтрация с одним условием и сортировка отфильтрованных данных
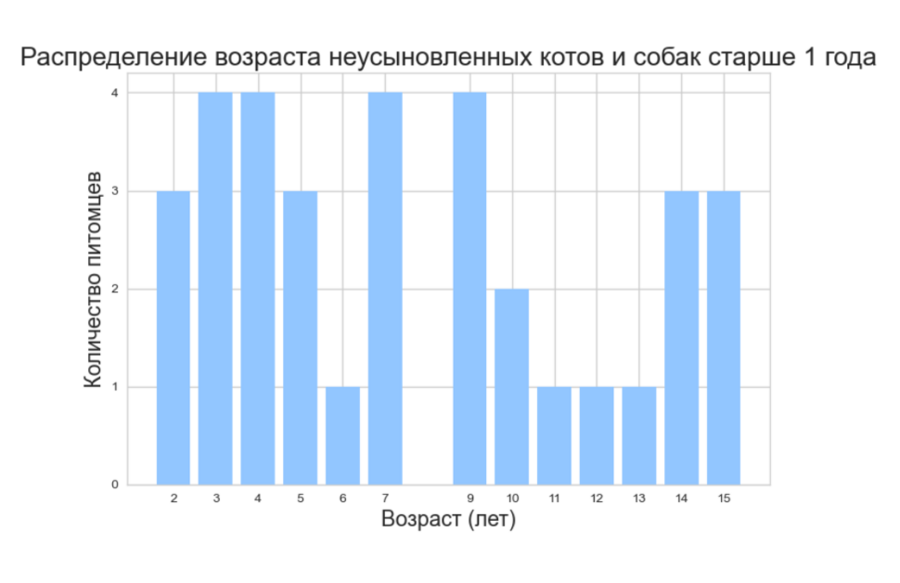
Фильтрация одновременно по нескольким условиям и сортировка отфильтрованных данных
Новые признаки
Создание нового признака в данных с помощью анонимной функции
Создание нового признака в данных с помощью именной функции
Сводные таблицы
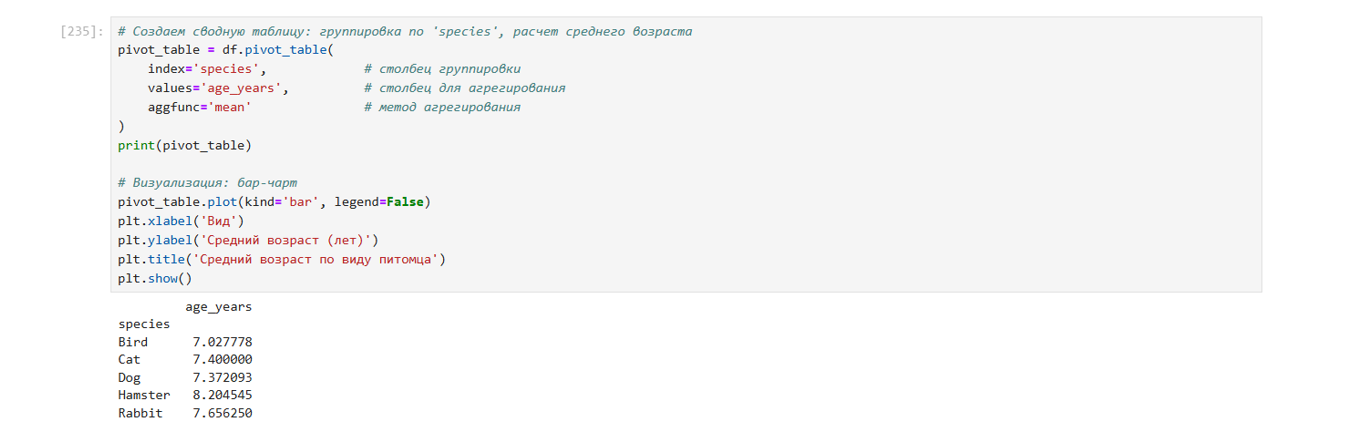
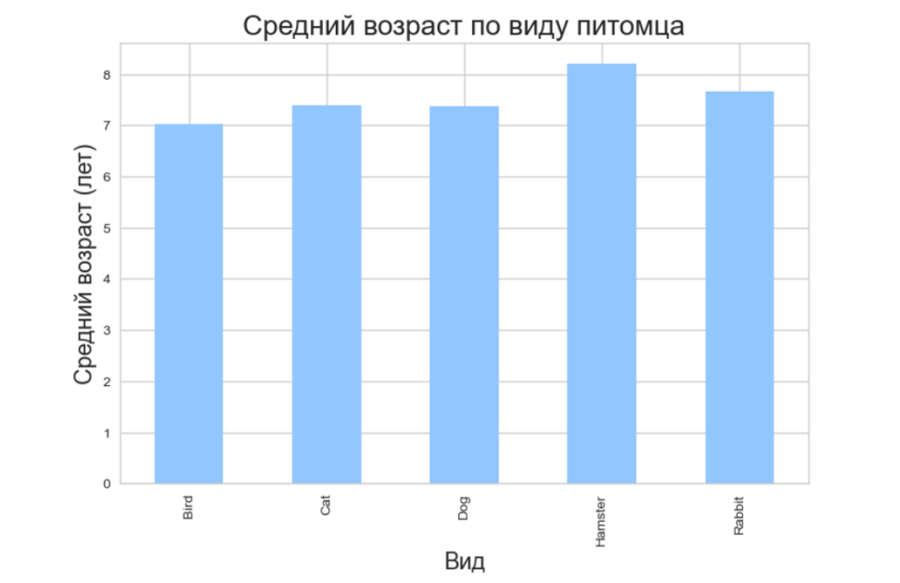
Сводная таблица: один столбец группировки, один столбец агрегирования, один метод агрегирования
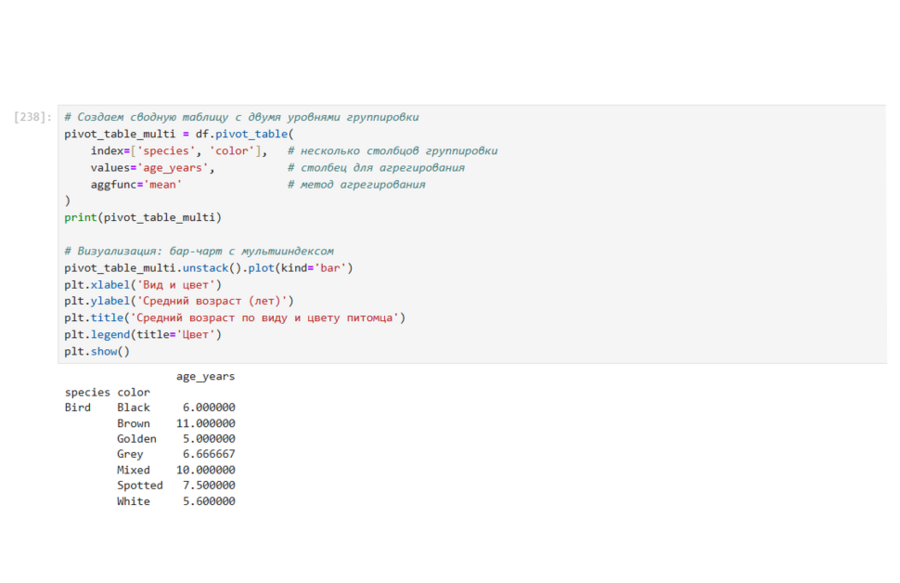
Сводная таблица: несколько столбцов группировки, один столбец агрегирования, один метод агрегирования
Сводная таблица: одни столбец группировки, несколько столбцов агрегирования, один метод агрегирования
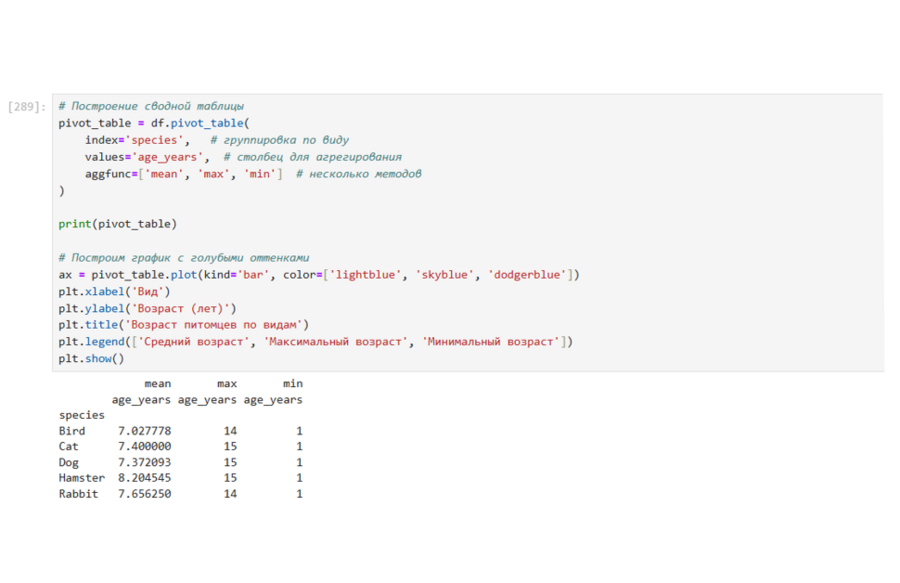
Сводная таблица: одни столбец группировки, один столбец агрегирования, несколько методов агрегирования
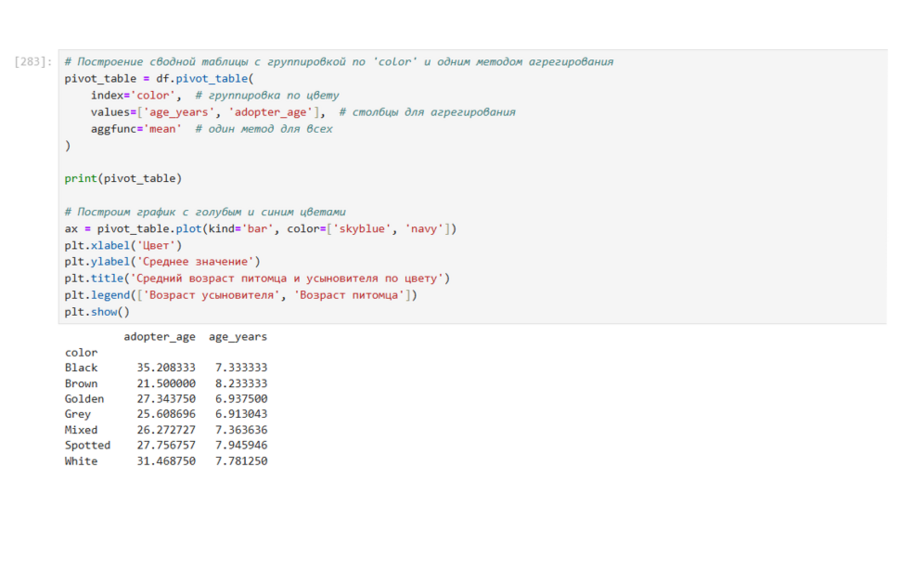
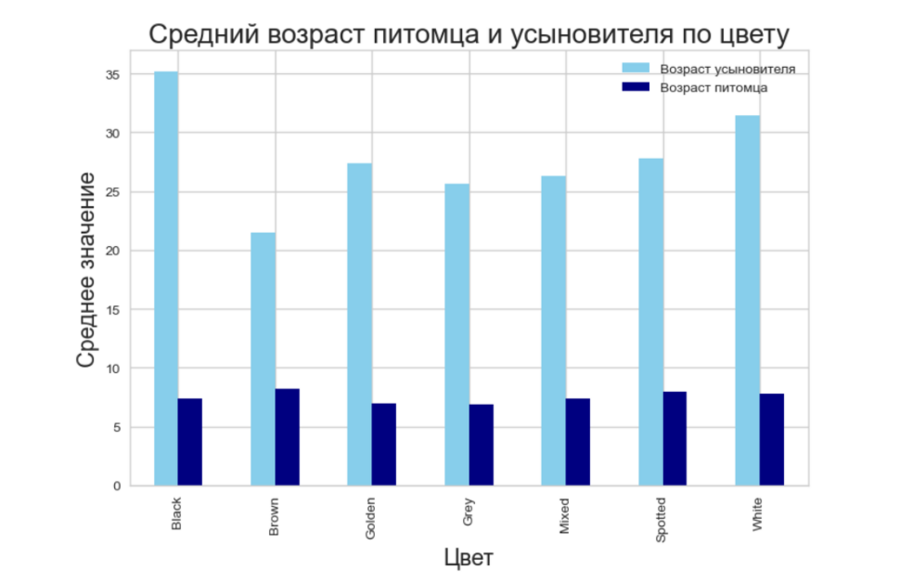
Сводная таблица: одни столбец группировки, несколько столбцов агрегирования, несколько методов агрегирования
Замена пропусков и удаление выбросов
Замена пропусков
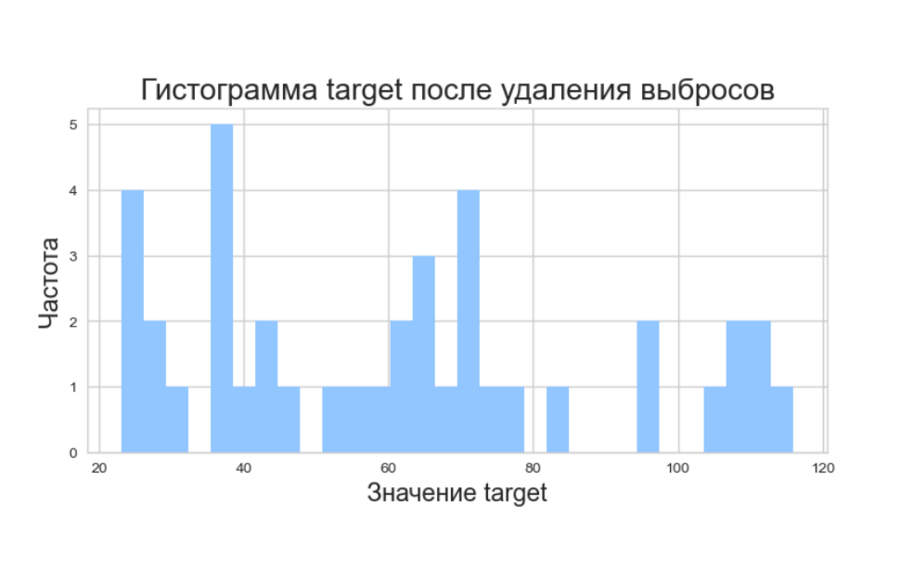
Использование метода N стандартных отклонений для целевой переменной
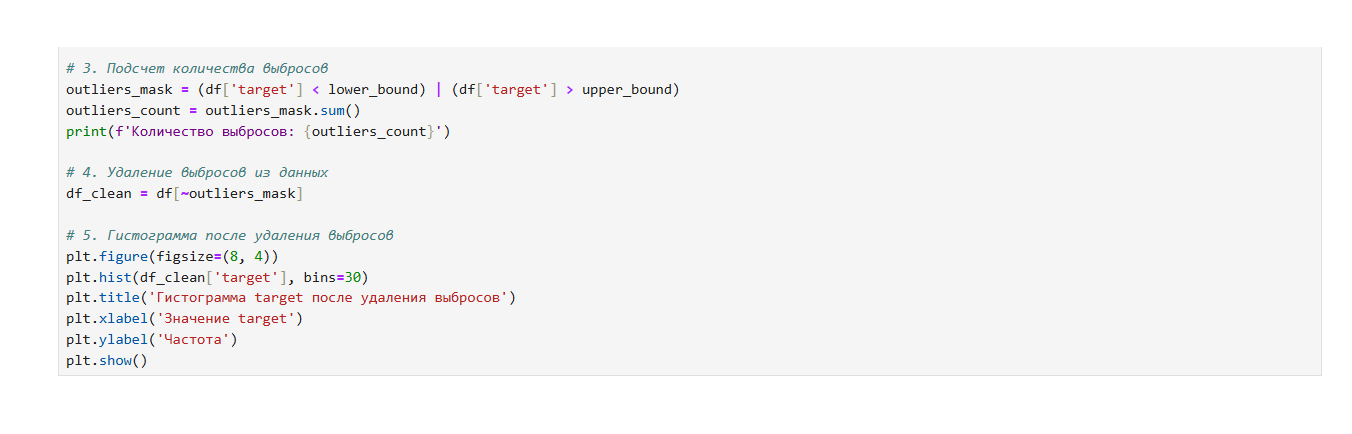
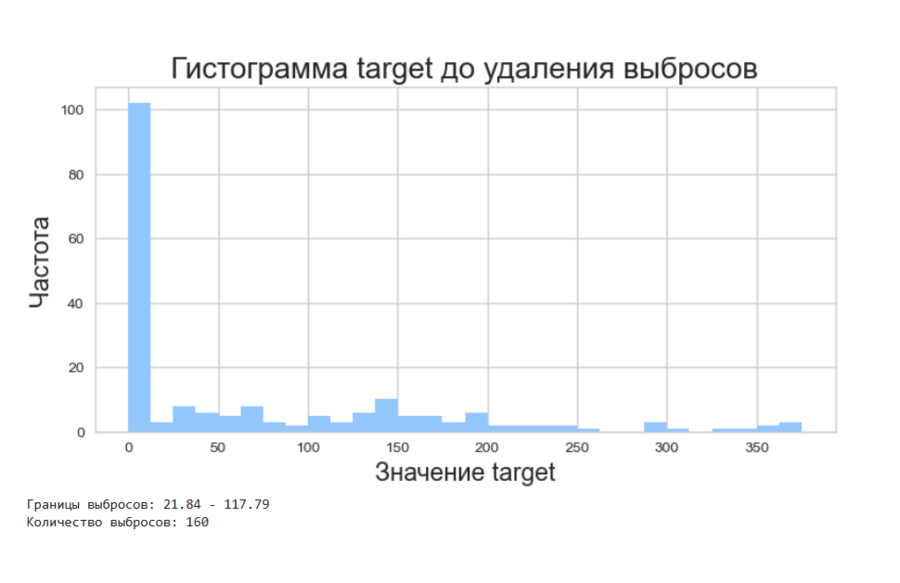
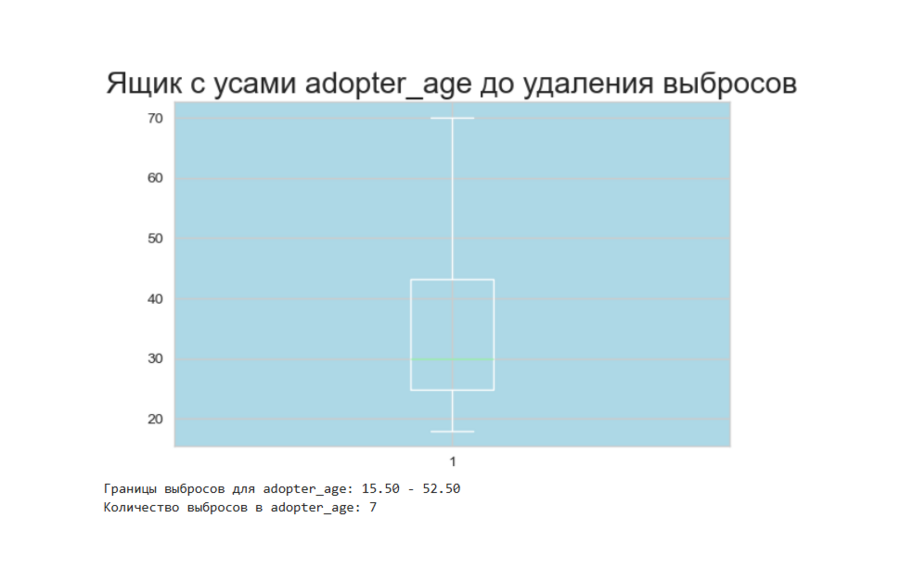
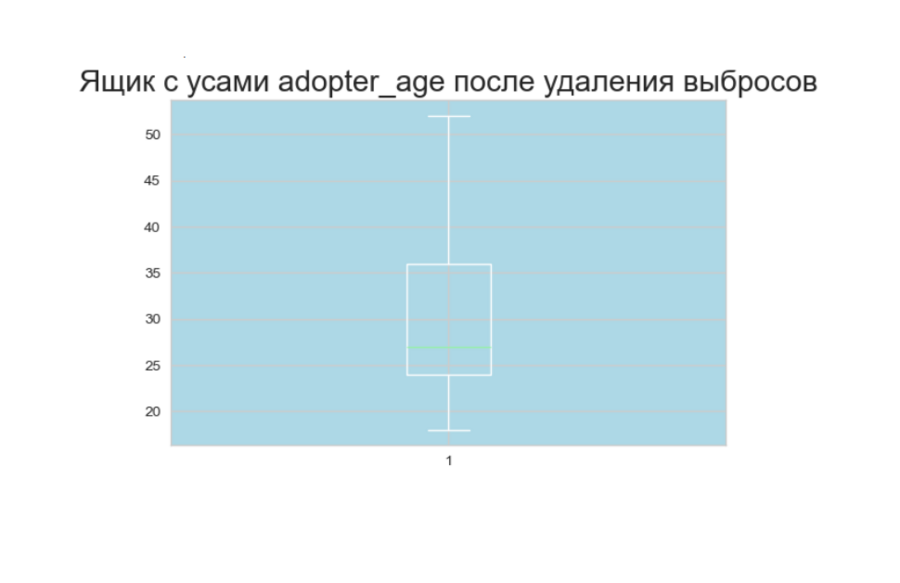
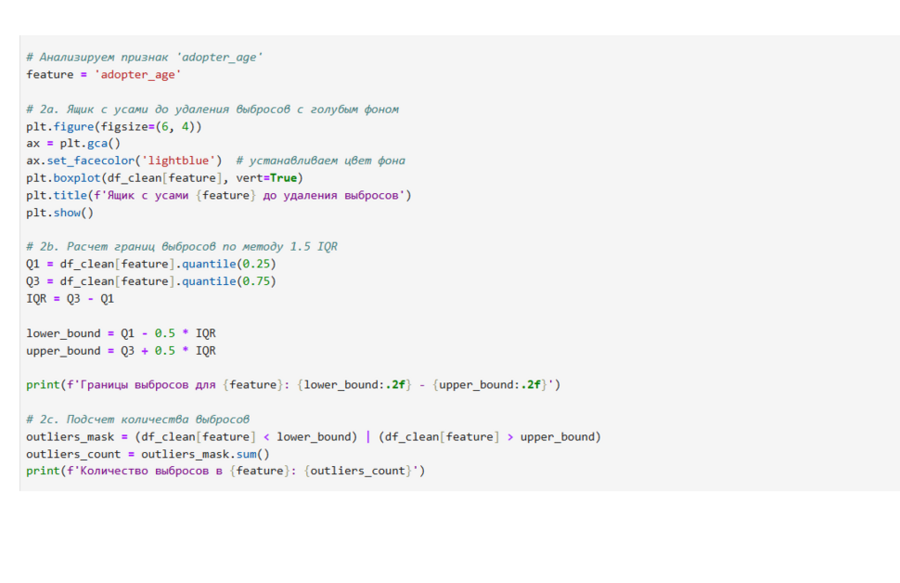
Использование метода 1.5IQR для предиктора или другого количественного признака (не целевого):
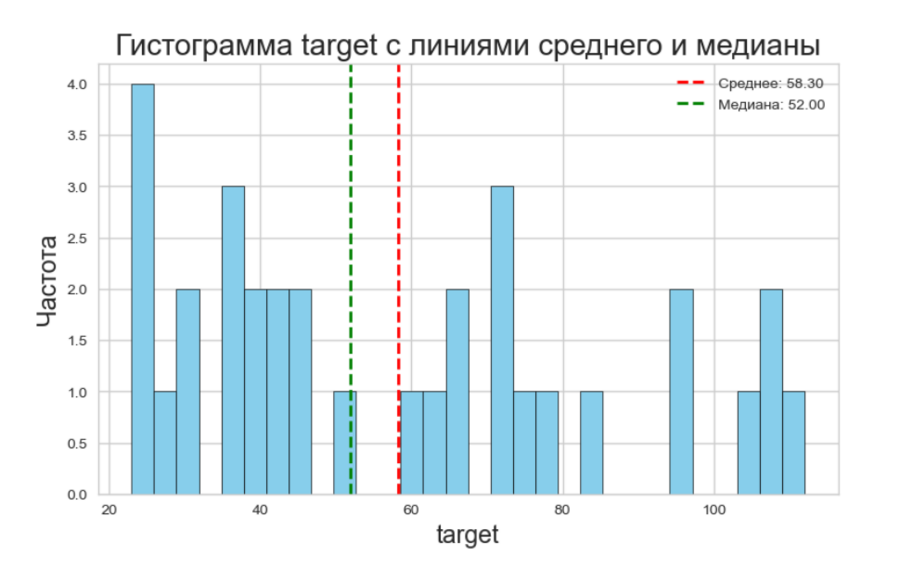
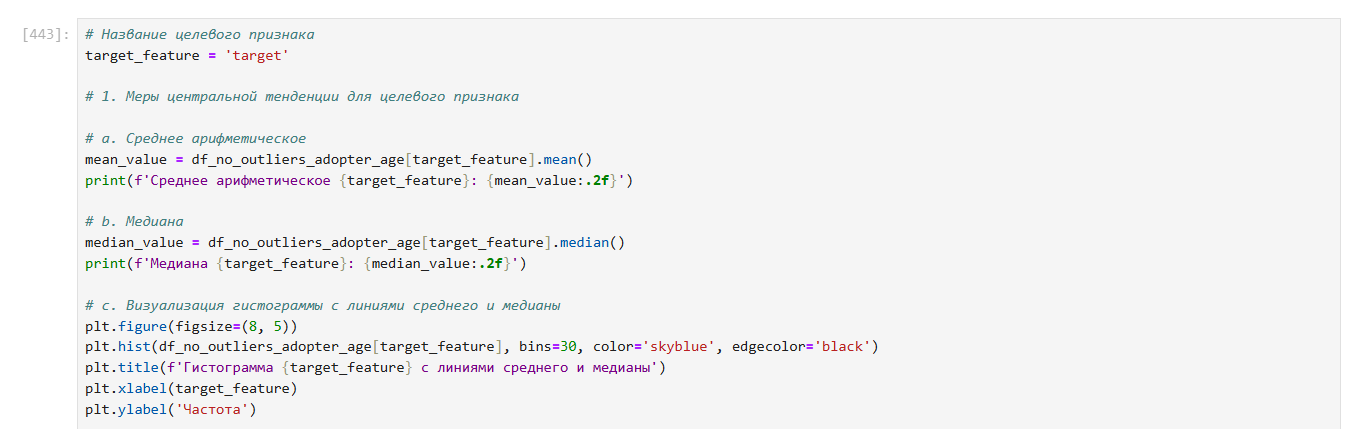
Меры центральной тенденции целевого признака:
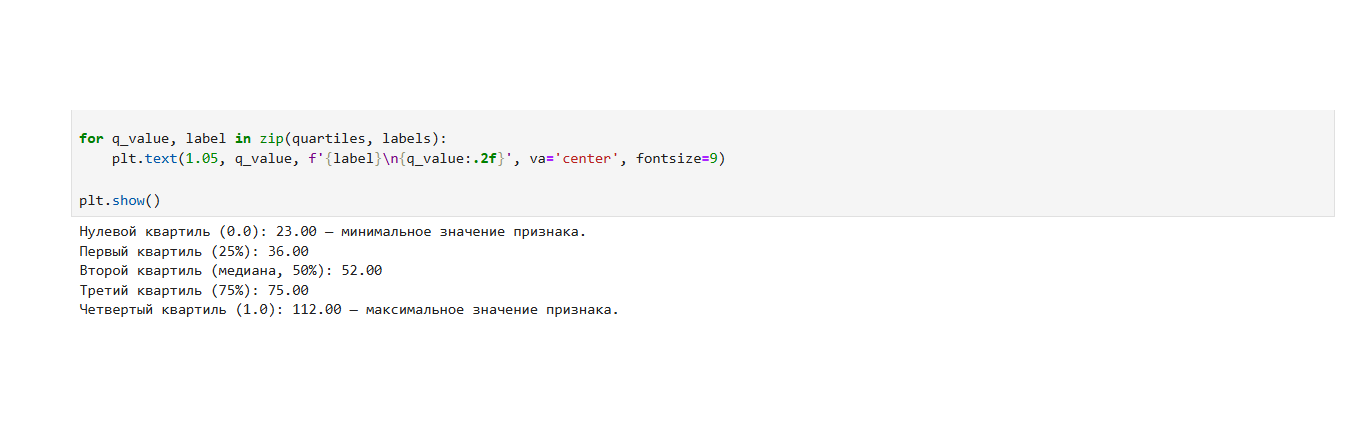
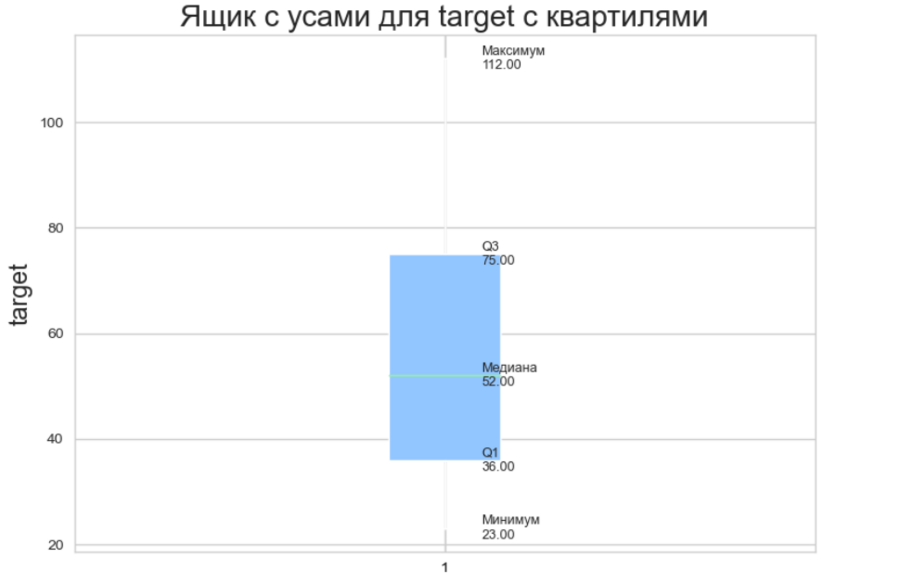
Квартили целевого признака:
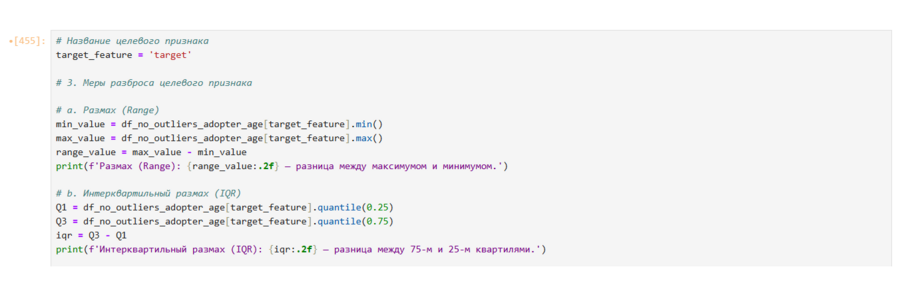
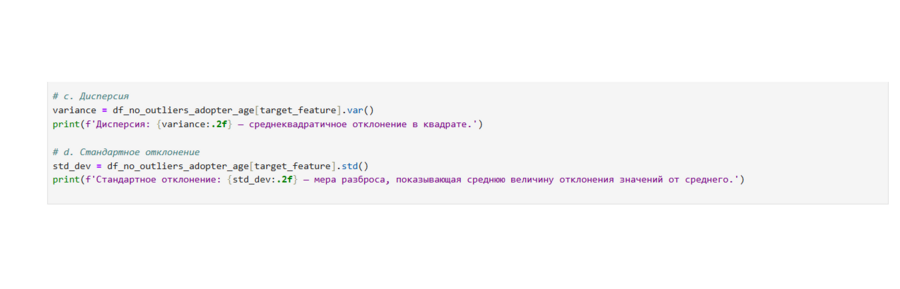
Меры разброса целевого признака
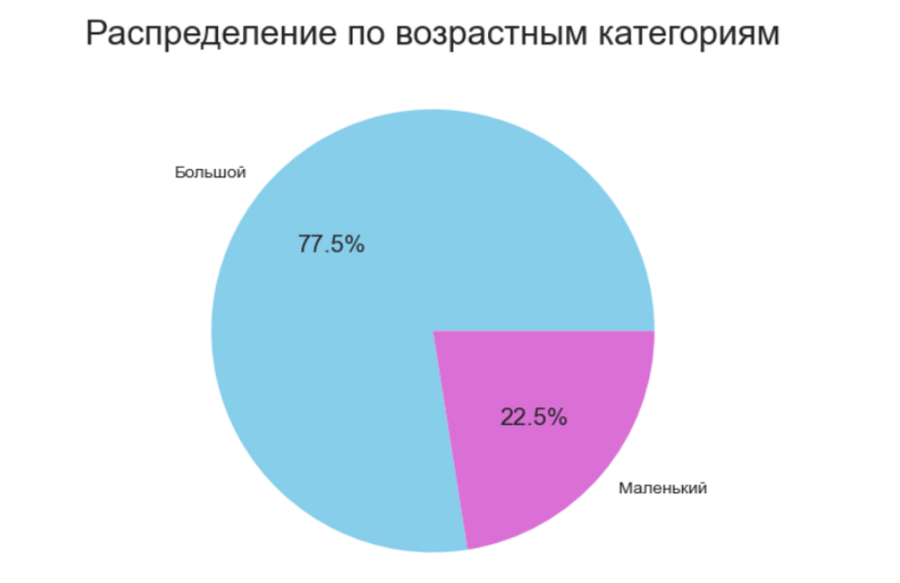
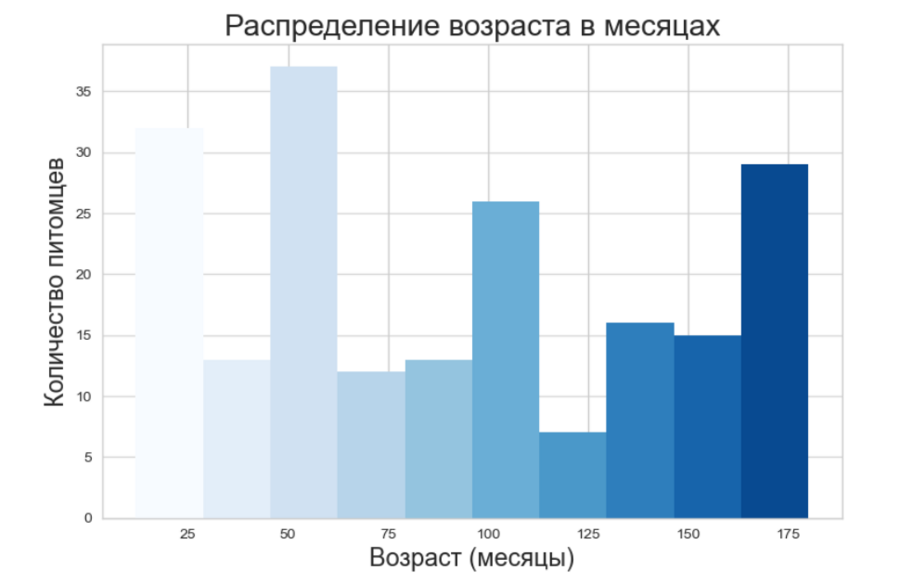
Описание категориального признака
Корреляция Пирсона
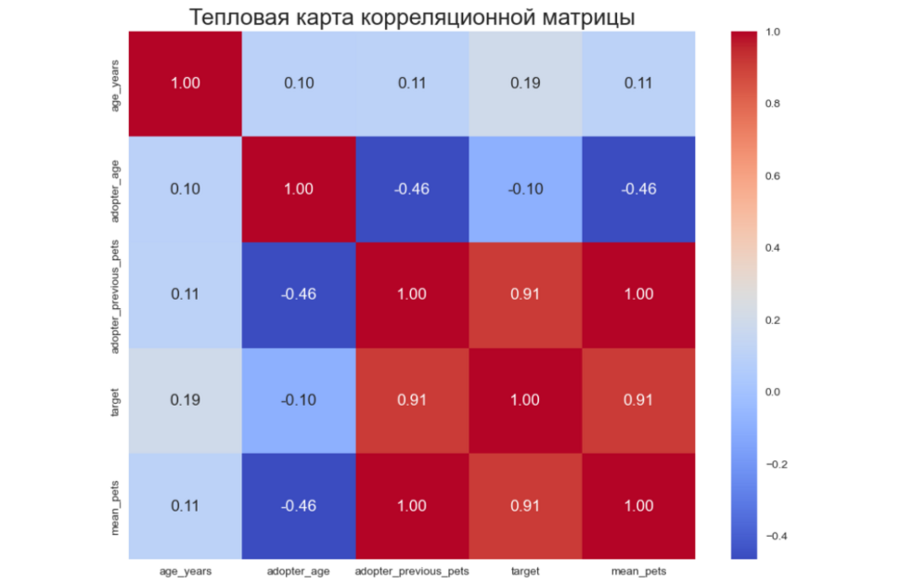
Визуализация корреляционной матрицы с помощью тепловой карты
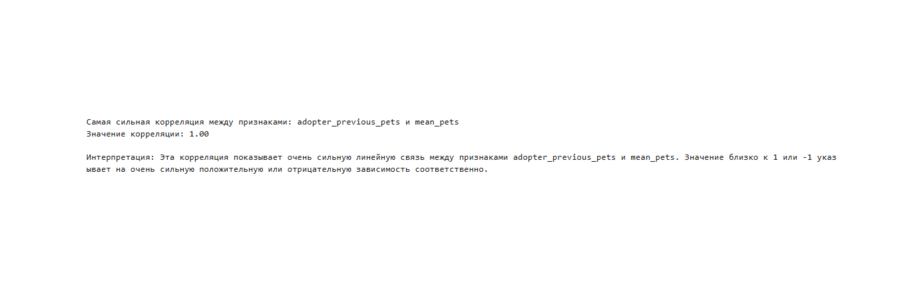
Интерпретация самой сильной корреляции между признаками, по тепловой карте
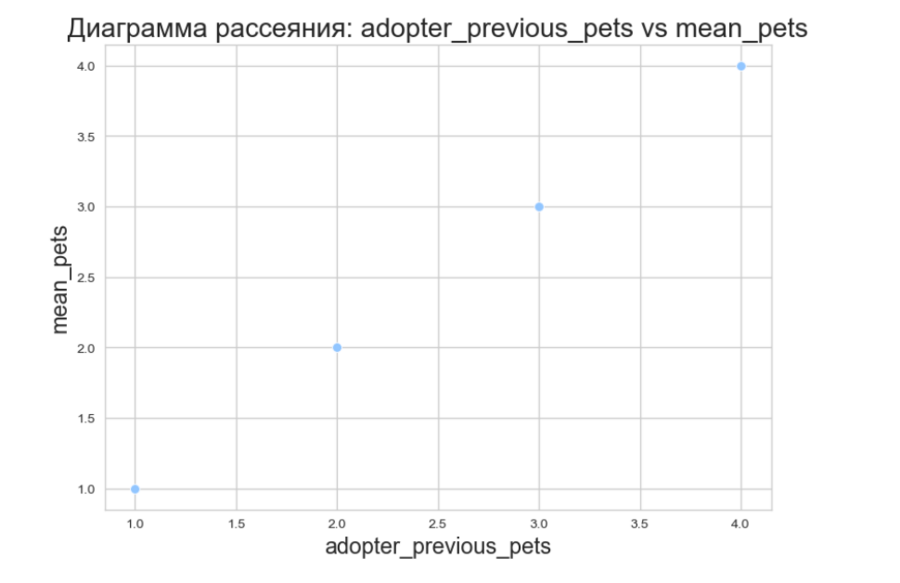
Построение диаграммы рассеяния между признаками, у которых самая сильная корреляция
Модель парной (простой) линейной регрессии предполагает, что значение целевого признака adopter_age можно предсказать как линейную функцию признака age_years, то есть, что изменение age_years на единицу приводит к изменению adopter_age на определённое постоянное значение, с учетом случайных ошибок.
Y = b₀ + b₁X, где Y — зависимая переменная, X — независимая переменная, b₀ — свободный член (тоже, что и точка пересечения с осью Y), а b₁ — коэффициент регрессии, показывающий изменение Y при изменении X на единиц
2. Уравнение парной линейной регрессии Общий вид уравнения:
adopter_age^ = b₀+b₁×age_years где: b₀ — свободный член (пересечение с осью Y), b₁ — коэффициент наклона (показывает, насколько в среднем изменяется adopter_age при увеличении age_years на 1)