Раздел посвящен изучению основ работы с VEX — встроенным языком программирования в Houdini FX, который позволяет управлять геометрией и атрибутами через код.
В ходе занятия студенты научатся использовать базовые конструкции, работать с атрибутами и переменными на разных уровнях геометрии, применять условия и циклы, а также создавать пользовательские контроллеры для более удобной настройки параметров.
Референсы
В этом разделе мы завершим работу над ассетом и создадим композицию с использованием вариаций итоговой модели.


GOAT 1. Golden Hour / Dearme. Sacred Secret
Прежде чем перейти к финализации модели и созданию лэйаута, разберем основные инструменты и принципы, которые понадобятся для управления геометрией на этапе сборки сцены.
Attribute Wrangle
При написании VEX кода для работы с геометрией чаще всего используется Attribute Wrangle. Работая с этой нодой, важно выбрать верный режим (Run Over) — разные режимы предназначаются для работы с разными уровнями геометрии:
- Detail (Serial Mode) — код исполняется один раз
- Points/Primitives/Vertices (Parallel Mode) — код запускается на каждой точке / вершине / примитиве одновременно, это параллельный процесс
Чтобы увидеть разницу в работе этих режимов, создадим короткий код, выводящий в консоль координаты текущей точки. Создадим Attribute Wrangle, подключим любую геометрию в качестве входных данных, исполним выражение поочередно в Serial и Parallel Mode, и сравним результаты:
vector point_position = point(0, «P", @ptnum); printf(«position X = %s\n», point_position.x);
Basic Assignments
Мы уже знакомы с атрибутами как способом хранения данных в точках, примитивах и других элементах геометрии. VEX позволяет создавать и изменять эти атрибуты напрямую: для того чтобы создавать или объявить атрибут, достаточно написать его в окне VEXpression в таком формате:
v@myVectorAttribute; f@myFloatAttribute; i@myIntegerAttribute; s@myStringAttribute;
При работе с встроенными (стандартными, уже существующими в Houdini) атрибутами, тип данных перед @ определять не нужно:
@P; @ptnum; @numpt;
Как и в других языках программирования, основанных на C, в VEX можно легко выполнять все стандартные арифметические действия. Например, градиент-маску для использования в шейдинге можно быстро создать с помощью простого выражения:
f@mask = float(@ptnum)/@numpt;
Attributes & Variables
Работая с VEX, важно понимать разницу между атрибутами и переменными:
- Атрибуты — это данные, которые прикреплены к геометрии. Например, @P (позиция точки) или @Cd (цвет)
- Переменные — это временные значения внутри Wrangle, которые не существуют вне ноды, исполняющей код
Например, при необходимости рассчитать угол изгиба стебля, можно записать в Attribute Wrangle такой код:
float bend = fit01(rand(@ptnum), 10, 45); @bend = bend;
// float bend является локальной переменной, которая создаётся для расчёта и существует только внутри Attribute Wrangle // @bend является атрибутом, которому присваивается значение локальной переменной bend. Он сохраняется не геометрии и может быть использован в последующих нодах
Noise Functions
В качестве финального этапа работы над моделью, добавим мелкие детали, которые будут видны на крупных планах: прожилки, заломы и неровности. Опираясь на референсы выше, создадим похожий эффект с использованием Worley Noise с помощью функции wnoise() в ноде Attribute Wrangle.
В отличие от стандартной функции noise (), Worley Noise лучше подходит для имитации органических паттернов, так как формирует структуру из ячеек, похожую на сетку прожилок. Его формула выглядит так:
wnoise(position, &seed, &f1, &f2)
Функция wnoise () случайно размещает в трехмерном пространстве точки (feature points), а затем, на их основе, делит его на «ячейки». Знаком «&» отмечены переменные, значения которых возвращает wnoise () для каждой точки обрабатываемой геометрии:
- f1 — расстояние до ближайшей feature point
- f2 — расстояние до второй ближайшей feature point
int seed; float dist1, dist2; wnoise(@uv, seed, dist1, dist2); @P += dist1 * @N;
- В первых строках объявляются локальные переменные типов int и float
- Функция wnoise () вычисляет значения Worley Noise на основе @uv
- Последняя строка сдвигает точки геометрии на значение шума (dist1) вдоль нормали (@N)
Чтобы регулировать силу выдавливания паттерна, создадим локальную переменную amp, которая будет выступать в роли коэффициента:
float amp = 0.5; wnoise(@uv * amp, seed, dist1, dist2);
Так как прожилки имеют горизонтальный характер, добавим также векторный коэффициент freq, чтобы изменять частоту по трем осям независимо друг от друга:
vector freq = {5,1,1}; wnoise(@uv * freq, seed, dist1, dist2);
Чтобы найти наилучший вариант деформации, добавим возможность смещать шум за счет локальной переменной offset:
float offset = 5; wnoise(@uv + offset, seed, dist1, dist2);
В итоге, готовый код будет выглядеть так:
float amp = 0.1; vector freq = {5,1,1}; float offset = 5; int seed; float dist1, dist2; wnoise(@uv * amp * freq + offset, seed, dist1, dist2); @P += dist1 * @N;
UI Controls
Теперь, для более удобной настройки эффекта без необходимости ручного редактирования кода, можно вынести необходимые параметры в интерфейс ноды.
Пользовательские параметры можно объявить в Attribute Wrangle с помощью различных функций:
- chf («name») — для значений типа float
- chv («name») — для значений типа vector
- chi («name») — для значений типа int
- chs («name») — для значений типа string
В нашем случае, в параметры можно вынести amp, freq и offset, которые нужно будет часто изменять в ходе настройки внешнего вида модели.
float amp = chf(«amplitude»); vector freq = chv(«freq»); float offset = chf(«offset»); int seed = chi(«seed»);
wnoise (@uv * amp * freq + offset, seed, dist1, dist2); @P += dist1 * @N;
При использовании этих функции в коде, Attribute Wrangle автоматически предложит создать параметры в интерфейсе:
С добавлением пользовательских параметров в Attribute Wrangle, настраивать действие ноды станет удобнее. Кроме того, как и другие параметры, эти слайдеры позволяют создавать parameter references .
For Loops
Один из способов добиться более сложной и естественной деформации поверхности — многократное применение шума с накоплением результата. Такой подход позволит получить более реалистичный эффект, особенно если слегка изменять параметры деформации на каждом шаге цикла.
Для выполнения множества итераций однотипных действий с изменяемыми параметрами удобно использовать цикл for. В VEX его базовая структура выглядит так:
for (начальное значение; условие; шаг) { //Действие, пока выполняется условие }
Добавим эту конструкцию у уже готовому коду и укажем количество «слоев» шума в локальной переменной iter:
float amp = ch («amplitude»); vector freq = chv («freq»); float offset = chf («offset»); int seed = chi («seed»); float dist1, dist2; vector pos = @uv; int iter= chi(«number_of_iterations»);
for (int i = 0; i < iter; i++) { wnoise (pos* freq + offset + i, seed, dist1, dist2); @P += dist1 * amp * @N; }
// int i = 0 — это начальная инициализация счётчика. Переменная i создаётся внутри цикла и в первой итерации равна 0. Именно с неё начинается отсчёт количества повторений
// i < iter — это условие продолжения цикла
// i++ — это инкремент счётчика, то есть увеличение i на единицу при каждой итерации (аналогично записи i = i+ 1)
// внутри цикла переменная i используется в качестве дополнительного offset для Worley Noise
Get Values from Other Inputs


Чтобы добиться еще более естественной деформации, можно комбинировать несколько шумовых паттернов с разным масштабом и уровнем детализации. Попробуем сделать это, используя разные входы Attribute Wrangle.
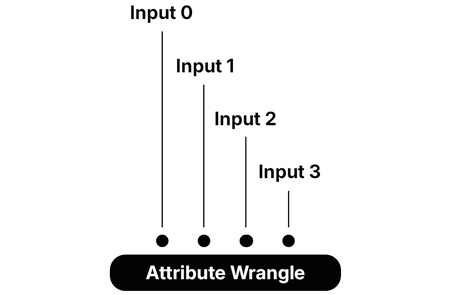
Attribute Wrangle, как и многие другие ноды, поддерживает несколько входов: по умолчанию используется первый (Input 0), но при необходимости можно обращаться и к другим, подключая дополнительные потоки данных для совместной обработки в одном коде.
vector pos = point (1, «P» ,@ptnum); @P = lerp (@P, pos, ch(«intensity»));
// В переменную pos записываются данные о положении (@Р) каждой точки (@ptnum), из второго входа (1) // Функция lerp () линейно интерполирует позиции точек из первого (@P) и второго (pos) входов, в соответствии с значением Intensity, который регулирует силу смешивания
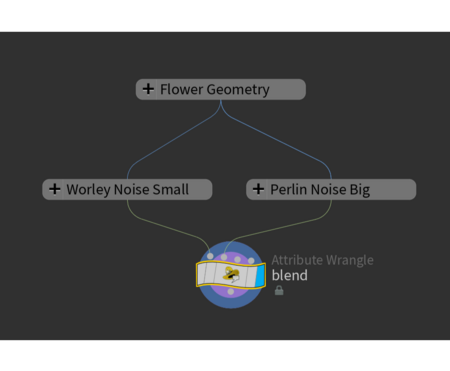

Для более точного соответствия референсу, крупные искажения следует оставить только на кончиках. Чтобы ограничить области воздействия шумов остается только добавить маску (f@blend):
vector pos = point (1, «P» ,@ptnum); @P = lerp (@P, pos, f@blend);
Условия в VEX: If Statement
Когда работа над детализацией закончена, соберем готовые модели в небольшую композицию, поместив их на несколько стеблей, созданных в ноде curve. Для того чтобы изолировать точки для копирования (вершины стеблей), необходимо создать условие: удалены должны быть все точки, кроме последних (по номеру) на каждой кривой.
Для процедурного удаления точек используем If statement:
If (условие) { // Действие, если условие истинно }
При необходимости, можно добавить альтернативное действие:
If (условие) { // Действие, если условие истинно } else { // Действие, если условие ложно }
В нашем случае условием будет удаление последней по номеру точки на каждом примитиве:
int pts[] = primpoints(0, @primnum);
int last = pts [len (pts)-1];
if (@ptnum != last) {
removepoint(0, @ptnum);
}
// С помощью primpoints () получаем массив всех точек, принадлежащих примитиву с номером @primnum
// В строке last = pts[len (pts)-1] получаем индекс последней точки на каждом примитиве, и записываем его в переменную last
// Функция removepoint () срабатывает для всех точек, кроме последних (@ptnum != last)
В завершение, с помощью конструкции «If…Else», поместим на точки модели бутонов. По итогам прошлого раздела мы экспортировали на диск несколько вариаций модели бутона:
- Bud_1 — закрытый;
- Bud_2 — полураскрытый;
- Bud_3 — полностью раскрытый;
Сначала вычислим наклон — это скалярное произведение между встроенным атрибутом точки @tangentu и вектором {0,1,0}, которое можно вычислить с помощью функции dot (). Результат запишем в переменную tilt:
float tilt = dot (@tangentu, {0,1,0});
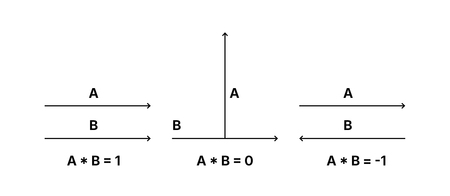
Так как диапазон значений tilt от -1 (вектора противоположны, кончик стебля смотрит вниз), до 1 (вектора сонаправлены, кончик стебля смотрит вверх), мысленно разделим его на три сегмента и добавим условие с использованием if Statement:
float tilt = dot(@tangentu, @up); int bud_variant;
if (tilt > 0.25) {
bud_variant = 3;
} else if (tilt > -0.25&& tilt <= 0.25) {
bud_variant = 2;
} else {
bud_variant = 1;
}
s@instancepath = sprintf ( "$HIP/Assets/Bud_%d.bgeo.sc" , bud_variant);
Так, s@instancepath на разных точках будет принимать значения:
- «$HIP/Assets/Bud_1.bgeo.sc» — для стеблей, ориентированных вниз
- «$HIP/Assets/Bud_2.bgeo.sc» — для слегка наклоненных стеблей
- «$HIP/Assets/Bud_3.bgeo.sc» — для стеблей, ориентированных вверх
Так, мы получаем завершенный ассет и основу для лэйаута:
Задание
Описание Финализируйте ассет и соберите лэйаут с использованием вариаций модели
Результат .hip-файл проекта
Ссылки



